Demystifying Formula Objects
I have done (and will hopefully do more) experiments with the formula object to try and better understand the behaviour. Hopefully this will help and inspire others to experiment also.
The formula object supplies two input values; u and v, which each have the range 0.0 to 1.0 and reflect the coordinates of a square grid lying on the x-y plane in the 3d view.
Carrara expects us to take the supplied u and v and calculate the output values of x y and z that directly represent the objects (local) 3d coordinate values in the Carrara 3d view.
So we use the u and v to calculate the x y and z.
Notice that even though we are only supplied a 2d point (u,v) we need to calculate a 3d point(x,y,z) So our formula needs to come up with the z value without a related input value.
NOTE See the "Using Formulas in Carrara" section for formula syntax and supported functions in the Carrara manual.
Setup
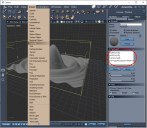
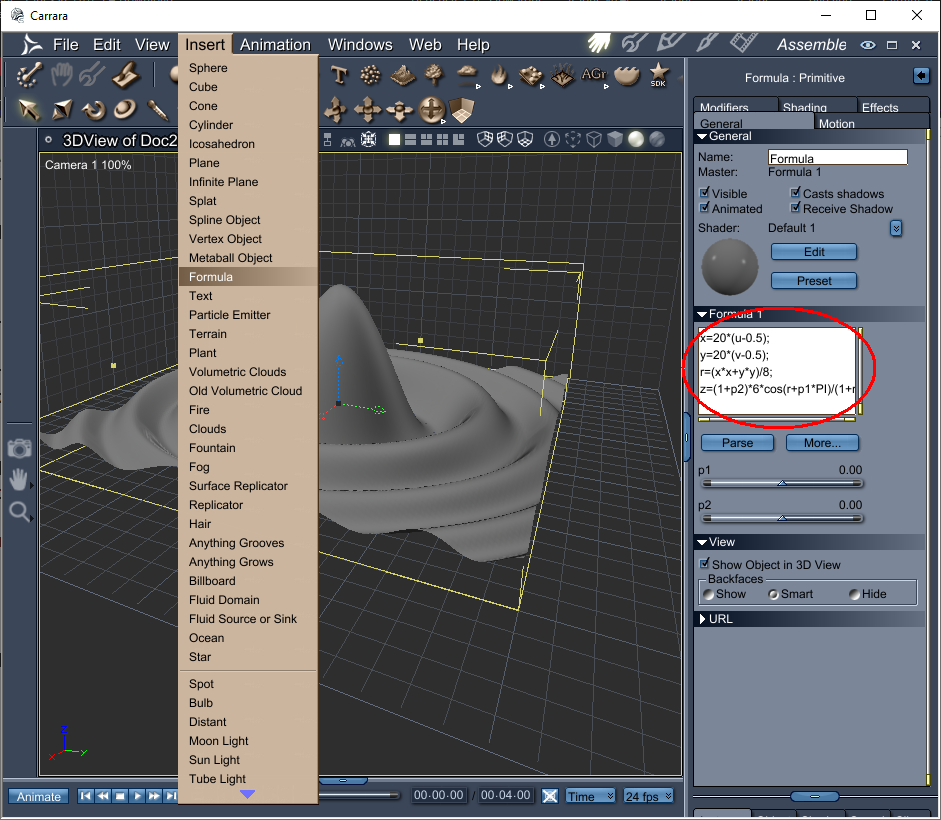
Insert a formula object and you can delete the default formula...
Experiment #1 - The uv's
Lets see the u,v grid supplied by Carrara using a very basic formula...
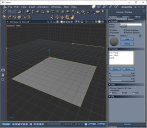
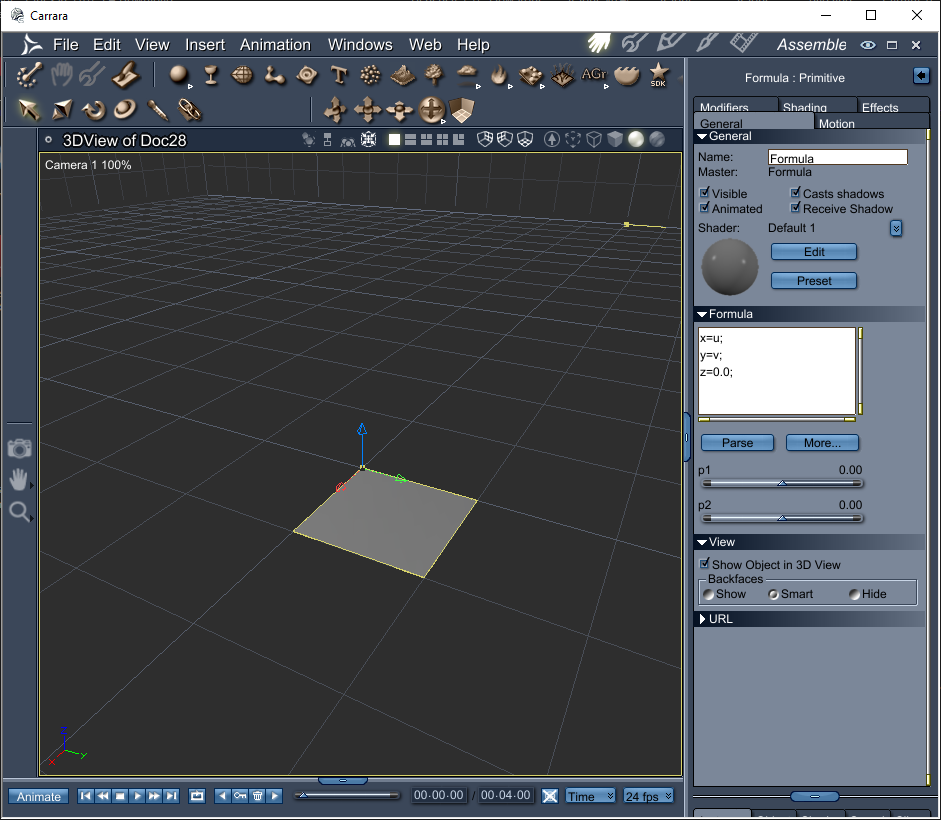
Here I set x=u, y=v, and just set z to 0
This gives a 1x1 grid object (since uv's only have the range 0.0 t0 1.0)
Note: This shows that Carrara calls our formula for each uv coordinate in the grid.
x=u;y=v;z=0.0;
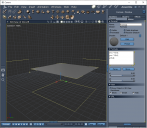
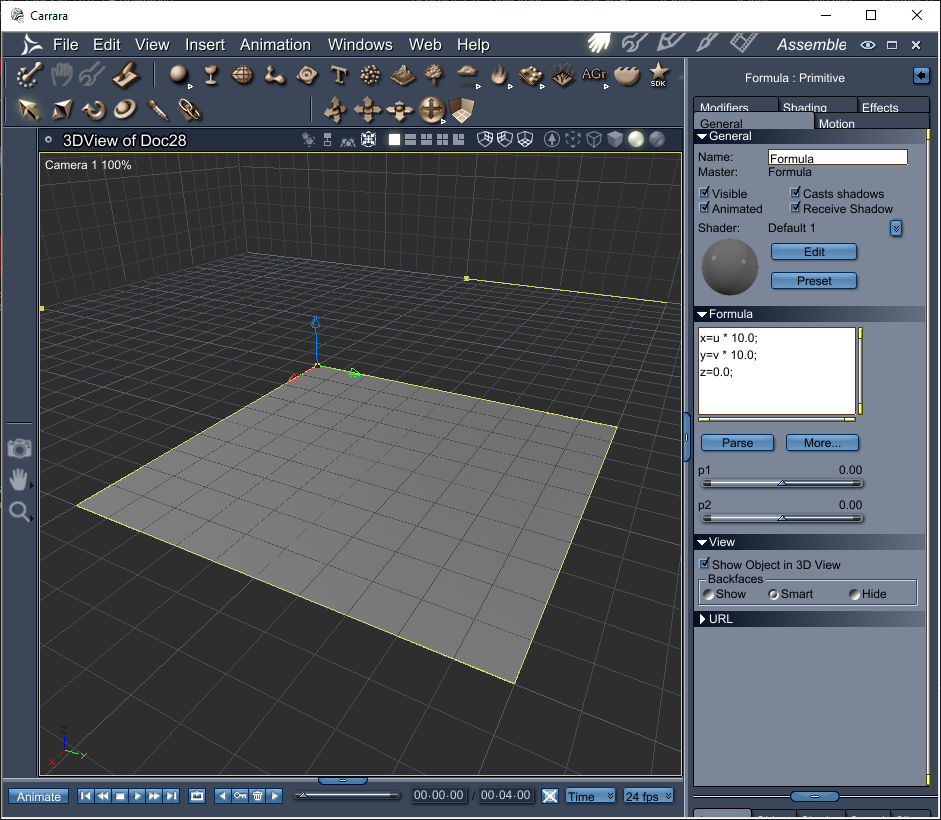
Experiment #2 - Scaling the uv's
The u and v values are scale independant which is why they only have a range of 0.0 to 1.0
because of this we can multiply them with whatever size we wish.
This gives a 10x10 grid object
x=u * 10.0;y=v * 10.0;z=0;Experiment #3 - uv resolution
I was curious to find out what the resolution of the uv box was. It turns out that if you convert either of the above objects to vector objects (at 100% fidelity) you get a grid with 16641 vertices. Which comes out to 129 u's and 129 v's. A very dense grid. Not sure if there is a way to change the uv resolution... but I imagine it is that dense for more complicated objects, you don't need a formula to create a square :)
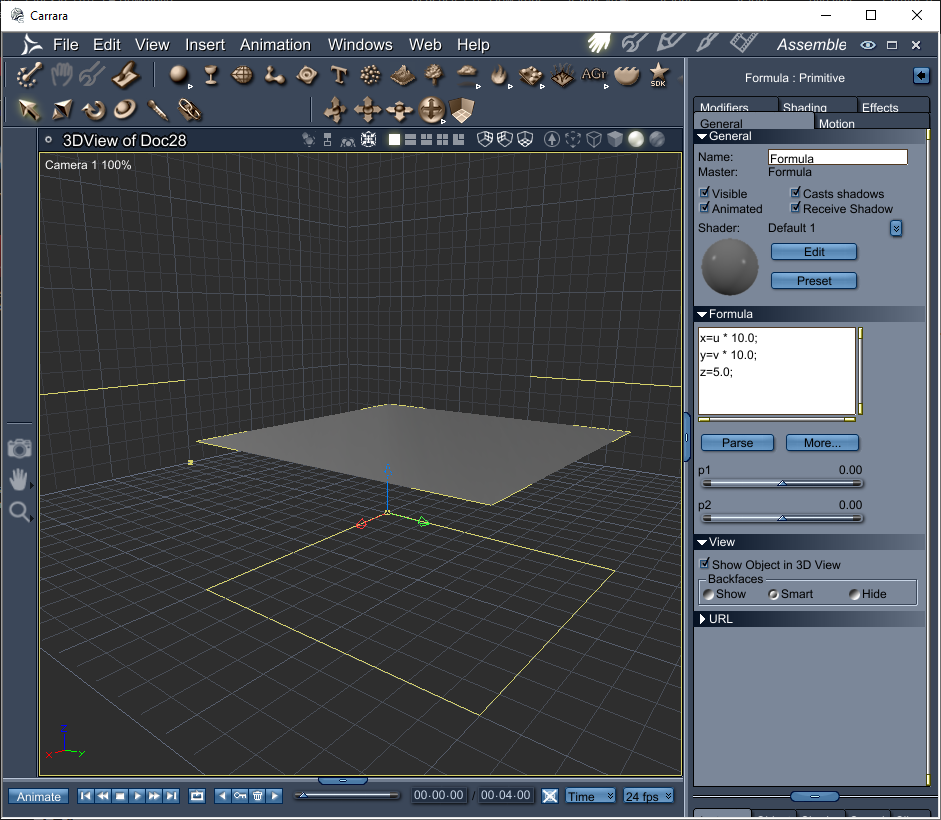
Experiment #4 - Lets do something with z.
Now that we have a basic idea of what is going on, lets change z to see what happens.
Setting z=5 will raise our grid up 5 units. Makes sense...
x=u * 10.0;y=v * 10.0;z=5.0;
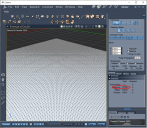
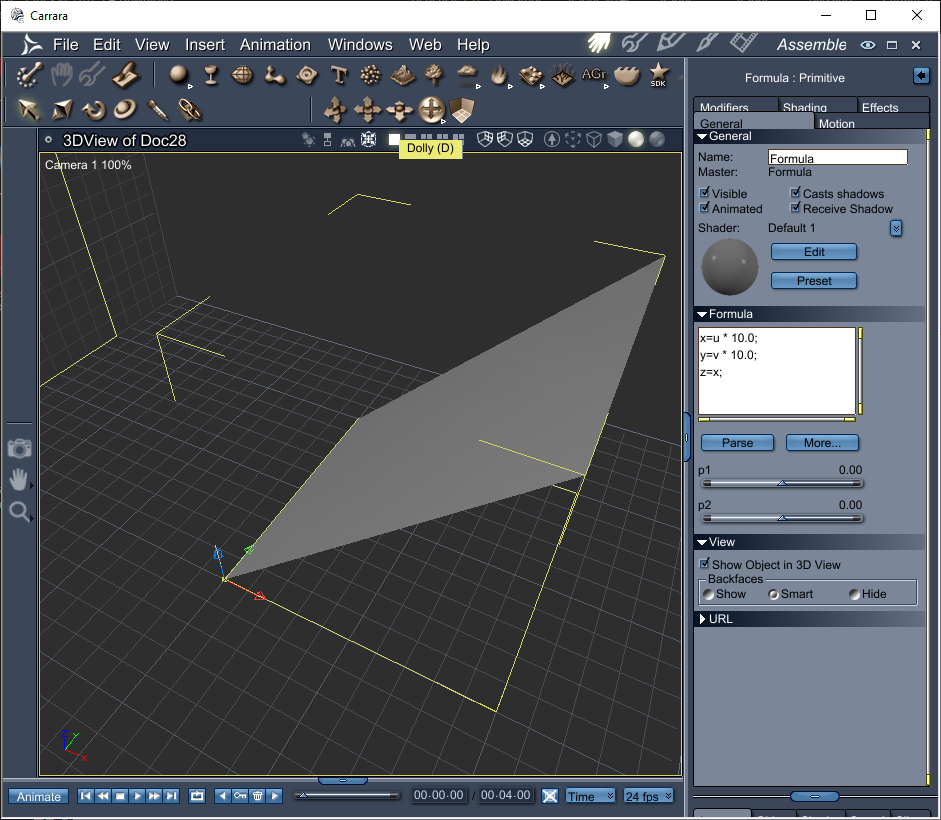
Experiment #5 - More better z
I will make z = x, so as x gets bigger so will z (thus our square should rise up in the x direction making a ramp)
x=u * 10.0;y=v * 10.0;z=x;More to come!
Feel free to comment/add/correct...









Comments
And here is an old thread with a few links, examples, and explanations
. - https://www.daz3d.com/forums/discussion/114716/formula-example
In particular, I recommend these two posts.
1) Using parameters to allow a torus formula (from French formula site) to have adjustable thickness
- https://www.daz3d.com/forums/discussion/comment/1598941/#Comment_1598941
2) General explanation of using a trig formula with pi to get a surface in Carrara
- https://www.daz3d.com/forums/discussion/comment/1599591/#Comment_1599591
Two more links
1) this is to another thread related to Carrara's formula object
https://www.daz3d.com/forums/discussion/30859/formula/p1
2) a reference from before Daz owned Carrara, posted by Pjotter
EDIT - bummer - looks like the link provided by Pjotter is broken.
Note on resolution
In my experience, using a formula for an object reduces file size when saving a scene, loading, etc when compared to use of a spline model or vertex model for the same object. However, the formula object tends to increase render time. That is just my experience, which is not extensive. It does seem to fit Mschack's resolution point.
oh wow thanks Diomede!
thanks for that mschack :)
Experiment #6 - Duplicate Verts
Since your formula can define any x,y,z given the u,v i wanted to see what Carrara would do with duplicate vertices. This formula does a modulas 5 to the result which basically will limit the range of the x and y values from 0 - 5 and cause them to overlap once.
The resulting vertice count is 4096, which is expected if Carrara welds duplicates.
Also notice that when the overlap happens there is a return edge generated when the x/y coords return back to 0 to start the second pass. (this is my assumption...)
Experiment #7 - Multiple z values
So far we have only done a plane which more or less maps each u,v directly to x,y at a fixed z. The result will always be a single plane, but if you look at some of the default objects provided with Carrara, you will notice that they all have multiple z planes, or said differently, there is more than one z value at each u,v. This was a mystery for me until i understood that the x,y values don't necessarily have to map directly to the uv's given. I partially showed this in the last experiment by overlapping the x,y values once, Given this let's try to make the second plane from Exp#6 be at a different z.
Here we will change the z value using the conditional statement. When u < 0.5, z = 0.0, and when u >= 0.5, z = 5.0.
The result is expected, we have now two planes of 4096 vertices. Notice both planes are joined which means Carrara always trys to join subsequent vertices.
BTW keep in mind I may not have a clue what I'm talking about, I have already had to correct a couple mistakes...
Kindly tell me if you find anything that is not correct, I am figuring this out as I go. :)
This is why they are called "Experiments" and not "Lessons"
I went through the french site (that Diomede mentioned above) and created some of the formulas, some i added slider parameters. Attached is a folder that contains all the .car files in a zip.
Unzip the folder wherever you wish, then in the browser add that folder (see attached image "addfolder.png")
That's awesome, thank you very much mschack!
Part of this formula project is motivated by my search for abstract rendering ideas in Carrara... Perhaps i will make an "Abstract/Surreal Renders" thread.
Thank you, mschack. Somehow I missed your shared Zip file when it got posted. Much appreciated.