The "Einstein Tile" A geometric shape that does not repeat itself when tiled
Apparently the elusive "Einstein Tile" has been discovered and it is a 13-sided polykite shape that when tiled never repeats itself. This would seem to be good news for us, eventually.
https://phys.org/news/2023-03-geometric-tiled.html
https://www.sciencenews.org/article/mathematicians-discovered-einstein-tile

einstein_tile.jpg
1774 x 1088 - 245K


einstein_tile2.jpg
1440 x 810 - 312K
Post edited by FirePro9 on


Comments
That's really cool! Thanks for posting.
- Greg
huh
Interesting
I wonder how the guy came up with that. It's actually quite a simple shape, which is the most surprising.
designed by obviously someone who has never had to clean the mouldy grout on the bathroom floor
Thanks for the links FirePro9, it's a fascinating discovery!
That would make a great quilt!
Thanks
Being a Roger Penrose fanboi, I knew about Penrose Tiles , but this is even simpler.
, but this is even simpler. I wonder if having a prime number of sides(13) has any bearing on the mathematics of why it works.
I wonder if having a prime number of sides(13) has any bearing on the mathematics of why it works.
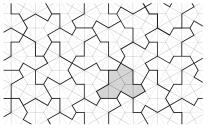
Is it just me or can nobody else see the pairs and triples in those images?
not adjacent
they shaded ones oriented the same way to illustrate that I think
it may repeat a couple randomly but it doesn't continue in a pattern
Those are quite "repetitive" and they all look like t-shirts hanging to dry.....
Repetition may seem to appear locally, but it's an illusion caused by our eye/brain's innate (but flawed) raison d'etre, to try to find patterns. I'm sure that close examination of all the other tiles around/inside a "repeating" pattern would find differences. If they've proved mathematically that it doesn't repeat, then it doesn't repeat.
I'm sure that close examination of all the other tiles around/inside a "repeating" pattern would find differences. If they've proved mathematically that it doesn't repeat, then it doesn't repeat. Of course that also depends upon one's defintion of repetition.
Of course that also depends upon one's defintion of repetition.
I think they're stylized teapots.
Very cool! Thanks for sharing. I love a bit of arty science. Now to scurry off and see how we can use this in 3D...
edited to add: I realize that the einstein tile is a 2D construct, and therefore it's application in 3D would be limited to texture tiling - pretty much how it would work in the design industry with fabrics, flooring, wallpapers. But I think it's still a fascinating concept and I'm looking forward to see where this may lead.
Use black grout. Then no-one, not even the householder, will see the mould. ;)
Interesting question. But the big question is I imagine, how to make the textures seamless.
The headlines on the articles are confusing if not misleading. It's not the shape that doesn't repeat, the point is that it is a single shape, it's that the pattern of how the shapes interlock doesn't repeat. This doesn't mean the same configuration exist either, it means that it won't occur at regular intervals as other patterns would. For example, you wouldn't be able to predict the same configurations repeating every X number of horizontal iterations of a pattern.
Cool mathematic stuff being hidden behind poorly worded headlines.
Um..., I think in this case, seamless is hopeless.
Probably. I'd rather think that fibonacci and other "natural" algorithms is the way to go - to imitate nature's seemingly chaotic randomness in a way that takes as little resources as possible. Procedural shaders also work quite well in many cases, like these:
https://www.daz3d.com/oso-shader-pack-1-for-iray
For fun I modeled 3 objs of the Einstein Tile "Hat". Per Wikipedia ( https://en.wikipedia.org/wiki/Einstein_problem ) the Hat is formed from 8 copies of a 60-90-120-90 kite, glued edge-to-edge and uses a mirror image as well (see attached image).
I would need a larger example to see if it's repetitive or not, for now I can see some repeating I marked one block of repe4at in green and the other in red, would need a larger one to see how the rest sorts in there but I have the impression it does sort
There wil be local repeats, but if you draw a bugger box then eventurally you will reach a point at which the pattern does not repeat. Just as an irrational number may recur for a bit but will then stop recurring.
I don't have the time or the engergy to follow up on the math of the article, that's why I thought it was a bit sad that there wasn't a larger sample which would visualise the thing. I can imagine it being like irrational numbers
I might take a plunge there, this weekend
ok I found this article in German:
https://www.spektrum.de/news/hobby-mathematiker-findet-lang-ersehnte-einstein-kachel/2124963
which contains this graphic which adresses the repetitive aspect I noticed and shows why it's not repetitive in the end
Also now I want a Penrose tiling for my DAZ rooms ... pretty please
Linwelly, that is an interesting article because it says that the lengths of the sides of the "Hat" can be varied, producing an infinite number of Einstein tiles. They include an animated GIF of the Hat shape morphing between a 7-sided comma shape and a 6-sided chevron shape. The chevron shape seems so much simpler, not sure why they are fixated on the Hat shape.
as I understood that gif both ends of the scale where the shape looses sides it as well looses it's function as einstein tile since they both clearly look repetitive
Oh, that makes sense, thanks for the clarification.
The cool thing, for our purposes though, is that if each of those tiles was a Patch of Grass, or a section of cobblestone, it would look a lot better and natural than the normal tiling Daz uses now and which the eye can find the pattern pretty quickly.
How do we generate such tiles for Daz Studio, then?
I also see how the pattern repeats, but maybe it is just related to the examples provided.
In Unity there are some methods to avoid repetitive texturing on the terrains or the other objects
and they work pretty well.